Positional Encoding

Transformer models do not contain recurrence or convolution. To enable the model to account for the order of the sequence, it is necessary to inject information about the relative or absolute positions of the tokens within the sequence. This positional information enhances the model’s sensitivity to positional variations, allowing it to effectively reason about the order of the input data.

In Transformer based models, a token is the fundamental unit of input data that the model processes. Tokens serve as the building blocks for the model’s input and can represent different levels of granularity, depending on the specific tokenization scheme employed. Once tokenized, these tokens are passed through an embedding layer, which transforms them into dense vector representations, known as embedding vectors. These embeddings are then fed into the Transformer model, along with positional information that is added to the input embeddings to provide information about the tokens’ positions in the sequence.

Positional encoding is a technique that Transformers use to keep track of input data order. Although there are a bunch of ways to do positional encoding, this post will focus on one widely used method proposed in Attention Is All You Need by Vaswani et. al. – the sinusoidal positional encoding.

Each input data point can have hundreds or even thousands of embedding values. Positional encoding functions by adding a sequence of numbers, corresponding to the order of the input data, to the embedding values of each data point (e.g., a word in a sentence or a point’s location in a polyline). These positional numbers are derived from a sequence of alternating sine and cosine squiggles with varying wavelengths:

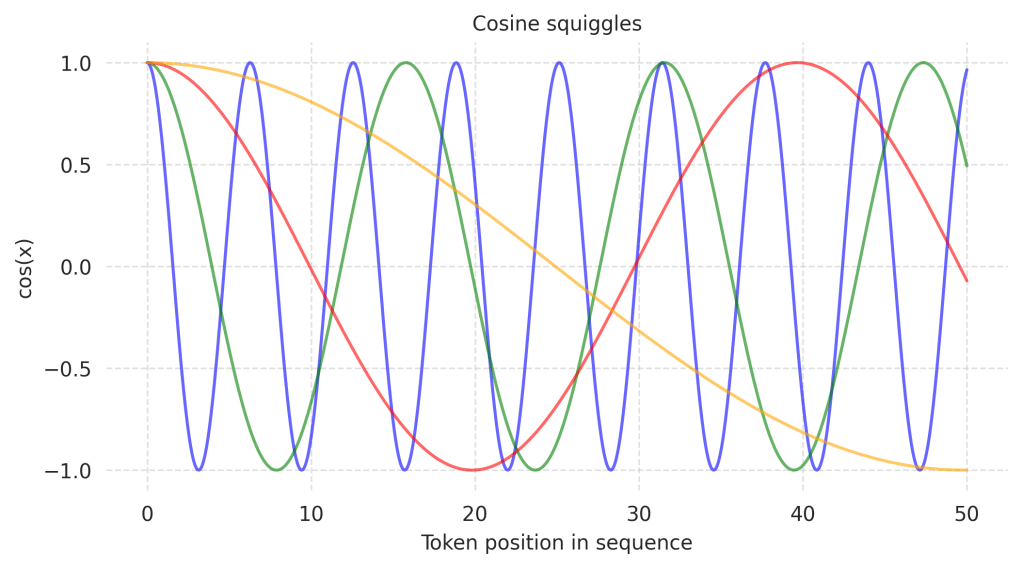
Each squiggle assigns a unique positional value to the embeddings of each input data point. For example, the y-axis values of the blue sine squiggle provide the positional encoding values for the first embedding of each input data point. Specifically, the positional value for the first embedding of the first data point corresponds to the y-axis coordinate of the blue sine squiggle at position 0, which is 0. Similarly, the positional value for the second embedding comes from the y-axis coordinate of the blue cosine squiggle at position 0, which is 1.

The green squiggles, which have longer wavelengths than the blue squiggles, provide positional values for the third and fourth embedding dimensions. For the first input data point, these values are 0 and 1, respectively, corresponding to the y-axis coordinates of the green sine and cosine squiggles. Thus, the positional values for the first input data point are derived from the y-axis coordinates of the respective squiggles at position 0.

For the second input data point, the process is the same, except the positional values are taken from the y-axis coordinates of the squiggles at the x-axis position corresponding to the second data point. This systematic approach ensures that each input data point receives a unique set of positional values based on its position in the sequence.

Due to the repetitive nature of sine and cosine squiggles, it is possible for two input data points to share the same position (or y-axis) values. However, since the squiggles have increasing wavelengths for larger embedding positions, the more embedding dimensions we use, the wider the squiggles become. As a result, even if occasional values repeat, the overall sequence of position values for each data point remains unique. This ensures that every input data point is assigned a distinct sequence of position values.

Now all we have to do is add the position values to the embedding values and we end up with the input data embeddings plus positional encoding for the whole sequence. The positional encodings have the same dimension d_model as the embeddings, so that the two can be summed. sine and cosine functions of different frequencies are defined as

$\bf{PE_{(pos,2i)}} = sin\left(\frac{pos}{T^{\frac{2i}{d_{model}}}}\right)$

$\bf{PE_{(pos,2i + 1)}} = cos\left(\frac{pos}{T^\frac{2i}{d_{model}}}\right)$

where pos is a position in the input sequence, i is a position in the embedding vector, and T is a scaling factor also sometimes called the temperature scale in the literature. In this post we set T=10000 as proposed in the paper referred above. As you can see, each dimension of the positional encoding corresponds to a sinusoid. The wavelengths form a geometric progression from $\bf{\pi}$ to $\bf{ 2 \pi \cdot T}$ .

The sinusoidal positional encoding has an ability to extrapolate to very long input sequences that might not be encountered during training. To leverage PyTorch’s GPU utilization and vectorization we need to modify the positional encoding equations. Specifically, we can modify the divisor using the logarithmic rules:

$\displaystyle \bf{\frac{1}{n^{\frac{2i}{d_{model}}}} = n^{-\frac{2i}{d_{model}}} = e^{log \left( n^{-\frac{2i}{d_{model}}}\right)} = e^{-\frac{2i}{d_{model}}log(n)} = e^{-\frac{2i \cdot log(n)}{d_{model}}}}$

Note that the sinusoidal position encoding can only be applied to even-dimensional token embeddings. Given that we need to raise a ValueError exception with an appropriate error message if it is odd.

import math
import torch

def sinusoidal_positional_encoding(max_length: int, d_model: int,
                                   n: float=10000.0) -> torch.Tensor:
    """Sinusoidal positional encoding.

    Args:
        max_length: max sequence length.
        d_model: embedding vector size.
        n: scaling factor.

    Raises:
        ValueError: if the given embedding size is not an even number.

    Returns:
        Positional encoding.
    """

    if d_model % 2:
        raise ValueError("Embedding size must be an even number!")

    div_term = torch.exp(torch.arange(0, d_model, 2) * -(math.log(n) / d_model))
    k = torch.arange(0, max_length).unsqueeze(1)

    pe = torch.zeros(max_length, d_model)
    pe[:, 0::2] = torch.sin(k * div_term)
    pe[:, 1::2] = torch.cos(k * div_term)

    return pe

Let’ put unit tests on this function. A unit test for testing input embedding size is straightforward:

import positional_encoding as pe
import torch
import math
import pytest

def test_sinusoidal_positional_encoding_embedding_size() -> None:
    """Test for different embedding sizes in the sinusoidal positional encoding."""
    max_length = 10

    # odd embedding size
    d_model = 5
    with pytest.raises(ValueError,
                       match=r"^Embedding size must be an even number!$"):
        _ = pe.sinusoidal_positional_encoding(max_length, d_model)

    # even embedding size
    d_model = 6
    _ = pe.sinusoidal_positional_encoding(max_length, d_model)

To test the values of the positional encoding, we need to define a helper function _theta for computing $\bf{\frac{pos}{n^{\frac{2i}{d_{model}}}}}$ , where pos is a position in the input data sequence, and i is a position in the embedding vector. This will help us to generate values, which will then be used for cross-checking in our tests. We define this function inside the unit test function for having a direct access to d_model variable:

def test_sinusoidal_positional_encoding() -> None:
    """Test for the sinusoidal positional encoding."""

    def _theta(pos_: int, dim_: int) -> float:
        """Helper function for calculating the internal value for sine and cosine.

        Args:
            pos_: position in the sequence.
            dim_: position in the embedding vector.

        Returns:
            The internal value for sine and cosine.
        """
        denominator = 10000. ** ((2 * dim_) / d_model)
        denominator = max(denominator, 1e-6)
        return pos_ / denominator

Let’s start by verifying our helper function with inputs for which the results can be easily calculated manually:

    max_length = 10
    d_model = 4

    assert _theta(pos_=0, dim_=0) == 0.
    assert _theta(pos_=0, dim_=1) == 0.
    assert _theta(pos_=0, dim_=2) == 0.

    assert _theta(pos_=1, dim_=0) == 1.
    assert _theta(pos_=1, dim_=1) == 0.01
    assert _theta(pos_=1, dim_=2) == 0.0001

    assert _theta(pos_=2, dim_=0) == 2.
    assert _theta(pos_=2, dim_=1) == 0.02
    assert _theta(pos_=2, dim_=2) == 0.0002

    assert _theta(pos_=3, dim_=0) == 3.
    assert _theta(pos_=3, dim_=1) == 0.03
    assert _theta(pos_=3, dim_=2) == 0.0003

Finally, we can test the positional encoding values:

    pos_encoding = pe.sinusoidal_positional_encoding(max_length, d_model)

    target_pos_encoding = torch.zeros(max_length, d_model)
    target_pos_encoding[0, 1::2] = 1.

    for pos in range(1, max_length):
        for dim in range(d_model // 2):
            theta = _theta(pos, dim)
            target_pos_encoding[pos, 2*dim] = math.sin(theta)
            target_pos_encoding[pos, 2*dim + 1] = math.cos(theta)

    assert pos_encoding.shape == torch.Size([max_length, d_model])
    
    # first row must match exactly
    torch.testing.assert_close(pos_encoding[0], target_pos_encoding[0],
                               rtol=0, atol=0)
    
    # next rows with some tolerance
    torch.testing.assert_close(pos_encoding, target_pos_encoding,
                               rtol=1e-4, atol=1e-4)

Note that we use torch.testing.assert_close for verifying that two tensors are numerically close to each other within a specified tolerance. This function is specifically designed for testing and debugging deep learning models, and it offers some advantages over traditional assertion methods:

it compares tensors while accounting for small numerical differences, that might be caused by rounding errors and / or hardware or optimization methods, by allowing configurable absolute atol and relative rtol tolerances.
it provides a detailed error message when the assertion fails. It shows the mismatched values, their locations, and the difference between the expected and actual tensors, which makes debugging easier compared to a generic assertion like assert.
it handles PyTorch-specific data types and devices (e.g., torch.float32, torch.float64, or tensors on GPUs) without requiring manual conversion, and works seamlessly with tensors on different devices (e.g., CPU vs. GPU), ensuring proper synchronization for comparison.
it supports tensor broadcasting, meaning you can compare tensors of different shapes if they are broadcast-compatible.
by default, the presence of NaN values in the tensors will fail the comparison. However, you can configure the behavior if needed (e.g., allow comparisons with NaNs).

In summary, torch.testing.assert_close is a robust, PyTorch-specific tool that simplifies and enhances the testing of tensor computations, making it ideal for deep learning workflows. You should consider using it in:

unit tests to verify the correctness of tensor outputs in model implementations or custom layers.
model regression tests to ensure no unintended changes in model outputs happen during updates.
numerical stability checks to validate results across devices (e.g., CPU vs. GPU) and / or environments (e.g., different PyTorch versions).

Coming back to our test function. Printing

    print(pos_encoding)
    print(pos_encoding.shape)

you should see

tensor([[ 0.0000,  1.0000,  0.0000,  1.0000],
        [ 0.8415,  0.5403,  0.0100,  0.9999],
        [ 0.9093, -0.4161,  0.0200,  0.9998],
        [ 0.1411, -0.9900,  0.0300,  0.9996],
        [-0.7568, -0.6536,  0.0400,  0.9992],
        [-0.9589,  0.2837,  0.0500,  0.9988],
        [-0.2794,  0.9602,  0.0600,  0.9982],
        [ 0.6570,  0.7539,  0.0699,  0.9976],
        [ 0.9894, -0.1455,  0.0799,  0.9968],
        [ 0.4121, -0.9111,  0.0899,  0.9960]])
torch.Size([10, 4])

I can already imagine you rolling your eyes and asking, why not integrate positional encoding directly into the PyTorch ecosystem? And you are totally right. Implementing a positional encoding as a PyTorch layer has several advantages compared to using precomputed or statically defined positional encodings, namely:

by defining positional encoding as a PyTorch layer, we encapsulate its logic within a single, reusable component. This makes it easier to integrate into models without repeating code. We can reuse the same positional encoding layer across different models or architectures by simply plugging it into our network.
A layer can compute positional encodings dynamically based on the input’s shape, making it suitable for varying sequence lengths. Instead of precomputing encodings for all possible sequence lengths, the layer can generate only the required encodings during runtime, saving memory.
When implemented as a PyTorch nn.Module, the layer automatically supports gradient computation (more on this in a second) and integrates with PyTorch’s autograd system. The positional encoding layer becomes part of the model, making it easier to save, load, and export the complete model (e.g., for ONNX or TorchScript).
an nn.Module easily supports device transfers (e.g., .to('cuda')) for GPU/TPU acceleration, with its parameters automatically transferring to the specified device.

from torch import nn

class PositionalEncoding(nn.Module):
    """Positional encoding class."""

    def __init__(self, d_model: int, max_length: int = 100,
                 n: float = 10000.) -> None:
        """Positional encoding initialization.

        Args:
            d_model: embedding vector size.
            max_length: max sequence length.
            n: scaling factor.
        """

        super().__init__()

        pe = torch.zeros(max_length, d_model)
        k = torch.arange(0, max_length).unsqueeze(1)
        div_term = torch.exp(
            torch.arange(0, d_model, 2) * -(math.log(n) / d_model))

        pe[:, 0::2] = torch.sin(k * div_term)
        pe[:, 1::2] = torch.cos(k * div_term)
        pe = pe.unsqueeze(0)

        self.register_buffer("pe", pe)

    def forward(self, x: torch.Tensor) -> torch.Tensor:
        """Forward pass.

        Args:
            x: input tensor (batch size x sequence length x embedding vector size).

        Raises:
            ValueError: if the given embedding size exceeds the positional encoding length.

        Returns:
            The tensor with added positional encodings.
        """
        if x.size(2) > self.pe.size(2):
            raise ValueError("Embedding size cannot exceed positional encoding length!")

        return x + self.pe[:, :, : x.size(2)]

Here we use register_buffer to register a tensor as a buffer within an nn.Module. Buffers are saved in state_dict and are part of the model’s state, but they are not considered trainable parameters. This makes them useful for storing values that should persist with the model (e.g., during saving and loading) but that should not be updated by gradient descent during training.

To make tests deterministic don’t forget to set a seed for generating random numbers on all devices in the test module:

torch.manual_seed(123)

The tests for the positional encoding layer look as

@pytest.mark.parametrize("embedding_size", [21, 40, 100])
def test_positional_encoding_wrong_embedding_size(embedding_size: int) -> None:
    """Test for the wrong embedding size in the positional encoding layer.

    Args:
        embedding_size: embedding vector size.
    """

    bs = 3  # batch size
    d_model = 20
    max_length = 10

    pos_encoding = pe.PositionalEncoding(d_model, max_length)
    input_embedding = torch.randn(bs, max_length, embedding_size)

    with pytest.raises(
        ValueError,
        match=r"^Embedding size cannot exceed positional encoding length!$"):
        _ = pos_encoding(input_embedding)


@pytest.mark.parametrize("embedding_size", [0, 1, 4, 20])
def test_positional_encoding(embedding_size: int) -> None:
    """Test for the positional encoding layer.

    Args:
        embedding_size: embedding vector size.
    """

    bs = 3  # batch size
    d_model = 20
    max_length = 10

    pos_encoding = pe.PositionalEncoding(d_model, max_length)
    input_embedding = torch.randn(bs, max_length, embedding_size)

    result = pos_encoding(input_embedding)

    assert result.shape == torch.Size([bs, max_length, embedding_size])
    torch.testing.assert_close(
        result - pos_encoding.pe[:, :, : input_embedding.size(2)],
        input_embedding, rtol=1e-6, atol=1e-6)

You can access the registered buffer with the positional encoding values like any other attribute of the module:

pos_encoding = pe.PositionalEncoding(d_model=4, max_length=10)
print(pos_encoding.pe)
print(pos_encoding.pe.shape)
print(pos_encoding.pe.requires_grad)

tensor([[[ 0.0000,  1.0000,  0.0000,  1.0000],
         [ 0.8415,  0.5403,  0.0100,  0.9999],
         [ 0.9093, -0.4161,  0.0200,  0.9998],
         [ 0.1411, -0.9900,  0.0300,  0.9996],
         [-0.7568, -0.6536,  0.0400,  0.9992],
         [-0.9589,  0.2837,  0.0500,  0.9988],
         [-0.2794,  0.9602,  0.0600,  0.9982],
         [ 0.6570,  0.7539,  0.0699,  0.9976],
         [ 0.9894, -0.1455,  0.0799,  0.9968],
         [ 0.4121, -0.9111,  0.0899,  0.9960]]])
torch.Size([1, 10, 4])
False

You could also incorporate dropout into your implementation, which randomly zeroes out some of the elements of its input with a given probability. This would help with regularization and prevent neurons from co-adapting (overrelying on each other).

Congratulations! By reaching this point, you now know how to implement sinusoidal positional encoding, integrate it into the PyTorch ecosystem, and test it effectively. I hope you found the read enjoyable and useful!

Cheers,
Alexey

References